Cho tam giác ABH vuông tại đỉnh H có góc ABH = 60^0. Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH = AB/2
Câu hỏi :
Cho tam giác ABH vuông tại đỉnh H có \(\widehat {ABH} = 60^\circ \). Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH = \(\frac{{AB}}{2}\).
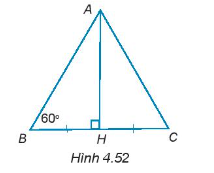
Cho tam giác ABH vuông tại đỉnh H có \(\widehat {ABH} = 60^\circ \). Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH = \(\frac{{AB}}{2}\).

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
+ Xét tam giác vuông ABH và tam giác vuông ACH có:
AH: cạnh chung
HB = HC (gt)
Do đó, ∆ABH = ∆ACH (hai cạnh góc vuông).
Suy ra AB = AC. (1)
Do đó, tam giác ABC cân tại đỉnh A.
⇒ \(\widehat C = \widehat B = \widehat {ABH} = 60^\circ \).
Ta có: \(\widehat {BAC} + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong tam giác).
Suy ra \(\widehat {BAC} = 180^\circ - \widehat B - \widehat C = 180^\circ - 60^\circ - 60^\circ = 60^\circ \).
Khi đó \(\widehat B = \widehat {BAC}\), do đó tam giác ABC cân tại đỉnh C nên AC = BC. (2)
Từ (1) và (2) suy ra AB = AC = BC.
Do đó, ∆ABC đều.
+ Vì H thuộc BC và điểm H nằm giữa điểm B và điểm C, hơn nữa HB = HC, do đó H là trung điểm của BC.
Suy ra \(BH = \frac{{BC}}{2}\).
Mà BC = AB (chứng minh trên).
Vậy BH = \(\frac{{AB}}{2}\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 7 Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng có đáp án !!
Copyright © 2021 HOCTAP247
