Trang chủ
Đề thi & kiểm tra
Lớp 7
Toán học
Trắc nghiệm Toán 7 Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án !!
Cho tam giác ABC có M, N lần lượt là...
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G.
Câu hỏi :
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng :
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
Đáp án đúng là: B
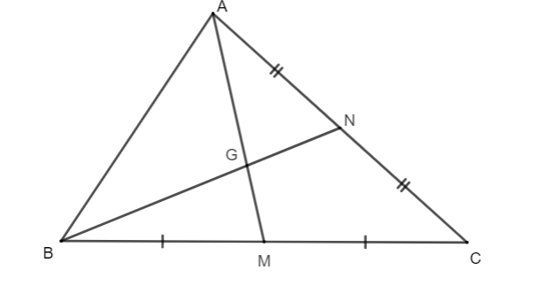
Xét ∆ABC có:
AM là đường trung tuyến (M là trung điểm của BC);
BN là đường trung tuyến (N là trung điểm của AC).
AM và BN cắt nhau tại G.
Do đó G là trọng tâm của ∆ABC.
Suy ra (1)
Ta có: AG = AM − GM
Thay vào (1) ta được:
− =
1 − =
= 1− =
Vậy = .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 7 Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
