Trang chủ
Đề thi & kiểm tra
Vật lý
Bộ đề thi minh họa môn Vật lí THPT Quốc gia năm 2022 có lời giải (34 đề) !!
Trên một bề mặt chất lỏng, tại hai điểm A...
Trên một bề mặt chất lỏng, tại hai điểm A và B có hai nguồn điểm, phát ra sóng
Câu hỏi :
Trên một bề mặt chất lỏng, tại hai điểm A và B có hai nguồn điểm, phát ra sóng kết hợp cùng pha nhau theo phương thẳng đứng với bước sóng . Biết . Gọi (C) là đường tròn nằm trên mặt nước với AB là đường kính; M là một điểm dao động với biên độ cực đại, cùng pha với nguồn nằm bên trong (C). Khoảng cách lớn nhất từ M đến trung trực của AB là
A.
B.
C.
C.
* Đáp án
A
* Hướng dẫn giải
Chọn A
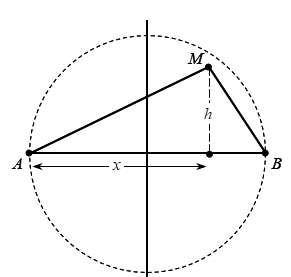
Để đơn giản, ta chọn . Vì tính đối xứng, ta chỉ xét các điểm thuộc phần tư thứ nhất của đường tròn.
Ta có:
o (1) (điều kiện cực đại cùng pha); n, k cùng tính chất chẵn lẻ.
o → (2).
o (điều kiện để M nằm ngoài AB) → (3)
o (4) (điều kiện để M nằm trong đường tròn).
Từ (1) và (4), ta có .
Để M xa trung trực của AB nhất thì nó phải nằm trên các cực đại bậc cao, do đó ta sẽ xét từ k=6 vào trong.
o → khi đó → trên dãy cực đại này không có điểm nào cùng pha với nguồn nằm trong đường tròn.
o → , tuy nhiên thì → do vậy để là thõa mãn.
→ , .
Từ hình vẽ, ta có:
o →
→ → .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ đề thi minh họa môn Vật lí THPT Quốc gia năm 2022 có lời giải (34 đề) !!
Số câu hỏi: 1301
Copyright © 2021 HOCTAP247
