Trong tất cả các hình nón nội tiếp trong hình cầu có thể tích bằng 36pi

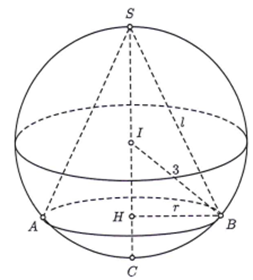
Vì hình cầu có thể tích bằng $36\pi$ nên bán kính hình cầu là R = 3.

Diện tích xung quanh của hình nón $S_{xq}=\pi rl.$

Gọi chiều cao của hình nón là h khi đó $h\in \left(0;6\right).$

Ta có $r^2=h.\left(2R-h\right)=6h-h^2,$ suy ra $r=\sqrt{6h-h^2}.$

Lại có $l^2=h.2R=6h,$ nên $S_{xq}=\pi \sqrt{6h-h^2}.\sqrt{6h}=\pi \sqrt{36h^2-6h^3}.$

Ta có $36h^2-6h^3=3h^2\left(12-2h\right)=3.h.h.\left(12-2h\right)\le 3.{\left(\frac{h+h+12-2h}{3}\right)}^3.$

Hay $36h^2-6h^3\le 192,$ dấu đẳng thức xảy ra khi h = 4.

Khi đó $r=\sqrt{6h-h^2}=2\sqrt{2}.$

Suy ra $S_{xq}$ lớn nhất bằng $8\sqrt{3}\pi$ khi $r=2\sqrt{2}.$