Cho hình chữ nhật ABCD tâm I, viết AB = a, AD = 2a. Gọi J là trung điểm BC

* Hướng dẫn giải

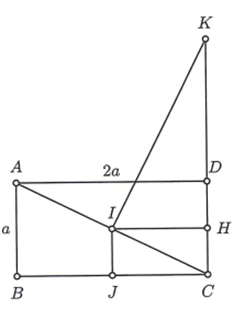
Gọi H là trung điểm CD nên tứ giác CHIJ là hình chữ nhật.

Khi cho tứ giác CKIJ quay xung quanh trục CK ta có:

Hình chữ nhật CHIJ tạo thành khối trụ có thể tích V₁

Tam giác IHK tạo thành khối nón có thể tích V₂

Suy ra: $V=V_1+V_2.$ Ta có

$V_1=\pi .C{J}^2.CH=\pi a^2.\frac{a}{2}=\frac{1}{2}\pi a^3,V_2=\frac{1}{3}\pi .H{I}^2.HK=\frac{1}{3}\pi a^2.HK.$

Xét tam giác vuông IHC có $IC=\sqrt{I{H}^2+H{C}^2}=\frac{a\sqrt{5}}{2};$

$$\begin{gathered} \tan \widehat{ICH}=\frac{IH}{CH}=2\Rightarrow IK=IC.\tan \widehat{ICH}=2.\frac{a\sqrt{5}}{2}=a\sqrt{5} \\ \Rightarrow HK=\sqrt{I{K}^2-I{H}^2}=\sqrt{5a^2-a^2}=2a. \\ Do vậy V_2=\frac{1}{3}\pi .H{I}^2.HK=\frac{1}{3}\pi a^2.2a=\frac{2}{3}\pi a^3. \\ Vậy V=V_1+V_2=\frac{1}{2}\pi a^3+\frac{2}{3}\pi a^3=\frac{7}{6}\pi a^3. \end{gathered}$$