Cho hình hộp ABCD.A'B'C'D' có đáy là hình thoi cạnh a và góc BAD = 60o

* Hướng dẫn giải

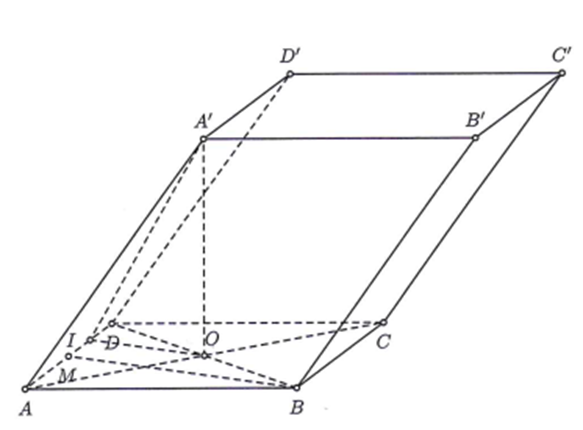
1. Vì tứ giác ACC'A' là hình thoi và góc $\widehat{A^{\text{'}}AC}={60}^{\text{o}}$  

nên tam giác AA'C đều.

Suy ra $A^{\text{'}}O\perp AC$  (với O là tâm của hình bình hành ABCD).

Mà $\left(AC{C}^{\text{'}}{A}^{\text{'}}\right)\perp \left(ABCD\right);\left(AC{C}^{\text{'}}{A}^{\text{'}}\right)\cap \left(ABCD\right)=\left\{AC\right\}.$

Do đó $A^{\text{'}}O\perp \left(ABCD\right).$

Gọi M là trung điểm AM $\Rightarrow BM\perp AD$ (tam giác  đều).

Gọi I là trung điểm MD $MD\Rightarrow OI\perp AD\Rightarrow$ góc giữa

hai mặt phẳng (BCC'B') và (ABCD) bằng $\widehat{A^{\text{'}}IO}.$

Ta có $AC=2AO=2.\frac{a\sqrt{3}}{2}=a\sqrt{3}.$

Xét tam giác AA'O vuông tại O có: $\tan \widehat{A^{\text{'}}IO}=\frac{A^{\text{'}}O}{OI}=2\sqrt{3}$

Xét tam giác BMD có: $OI=\frac{1}{2}BM=\frac{a\sqrt{3}}{4}.$

Xét tam giác A'IO vuông tại O có: $\tan \widehat{A^{\text{'}}IO}=\frac{A^{\text{'}}O}{OI}=2\sqrt{3}$

2. Ta có $S_{ABCD}=2S_{ABD}=2.\frac{1}{2}AB.AD.\sin {60}^{\text{o}}=\frac{a^2\sqrt{3}}{2};A^{\text{'}}O=\frac{3a}{2}.$

Vậy $V_{AC{B}^{\text{'}}{D}^{\text{'}}}=\frac{1}{3}{V}_{ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}=\frac{1}{3}.A^{\text{'}}O.S_{ABCD}=\frac{1}{3}.\frac{3a}{2}.\frac{a^2\sqrt{3}}{2}=\frac{a^3\sqrt{3}}{4}.$

3. Vì tam giác ABD đều nên tâm đường tròn nội tiếp tam giác

trùng với trọng tâm của tam giác  

=> Bán kính đường tròn đáy của hình nón là: $r=\frac{BM}{3}=\frac{a\sqrt{3}}{6}.$

Vì chiều cao của hình nón bằng chiều cao của lăng trụ nên ta có

độ dài đường sinh là $l=\sqrt{A^{\text{'}}{O}^2-r^2}=\sqrt{{\left(\frac{3a}{2}\right)}^2-{\left(\frac{a\sqrt{3}}{6}\right)}^2}=\frac{a\sqrt{159}}{6}.$

Vậy diện tích xung quanh của hình nón là: 

$S_{xq}=\pi rl+\pi r^2=\frac{\pi a^2\left(\sqrt{53}+1\right)}{12}.$