Cho số phức z thỏa mãn hệ phương trình |z - 1 - 2i| < = 1 và |z - 1 + 2i| > = |z + 3 - 2i|

* Hướng dẫn giải

Giả sử $z=x+yi\left(x,y\in ℝ\right)$.

Khi đó $\left|z-1-2i\right|\le 1\iff \left|\left(x-1\right)+\left(y-2\right)i\right|\le 1$

$\iff \sqrt{{\left(x-1\right)}^2+{\left(y-2\right)}^2}\le 1\iff {\left(x-1\right)}^2+{\left(y-2\right)}^2\le 1$.

Và $\left|z-1+2i\right|\ge \left|z+3-2i\right|$

$\iff \sqrt{{\left(x-1\right)}^2+{\left(y+2\right)}^2}\ge \sqrt{{\left(x+3\right)}^2+{\left(y-2\right)}^2}$

$\iff {\left(x-1\right)}^2+{\left(y+2\right)}^2\ge {\left(x+3\right)}^2+{\left(y-2\right)}^2\iff y\ge x+1$.

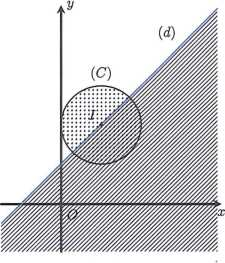
Gọi (T) là nửa mặt phẳng có bờ là đường thẳng d: y = x + 1,

không chứa gốc tọa độ O (0; 0). Khi đó tập hợp các điểm

biểu diễn số phức z thỏa mãn đề là nửa hình tròn (C) tâm I(1; 2),

bán kính R = 1 và thuộc (T). Vì đường thẳng d đi qua tâm

I(1; 2) của hình tròn(C) nên diện tích cần tìm là một nửa

diện tích hình tròn (C). Do đó $S=\frac{\pi }{2}$.