Cho hình lăng trụ đứng ABCD.A'B'C'D' với đáy là hình thoi có cạnh bằng 4a

Đáp án C

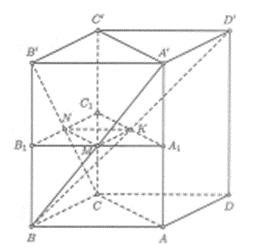
Gọi V là thể tích của khối lăng trụ $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$.

Gọi A₁, B₁, C₁ lần lượt là giao điểm của AA', BB', CC' và mặt phẳng (MNK).

Thể tích của khối lăng trụ ABC.A₁B₁C₁ là:

$V_{ABC.A_1{B}_1{C}_1}=\frac{1}{4}{V}_{ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}=\frac{1}{4}V$.

Gọi V₁, V₂, V₃ lần lượt là thể tích của khối tứ diện AA₁MK, BB₁MN, CC₁NK. Ta có

+) $V_1=V_{A.A_{1}MK}=\frac{1}{3}.S_{\Delta A_{1}MK}.A{A}_1=\frac{1}{3}.\frac{1}{4}{S}_{\Delta A_1{B}_1{C}_1}.A{A}_1$

          $=\frac{1}{12}{V}_{ABC.A_1{B}_1{C}_1}=\frac{1}{12}.\frac{1}{4}V=\frac{1}{48}$

+) $V_2=V_{B.B_{1}MN}=\frac{1}{3}.S_{\Delta B_{1}MN}.B{B}_1=\frac{1}{3}.\frac{1}{4}{S}_{\Delta B_1{A}_1{C}_1}.B{B}_1$

          $=\frac{1}{12}{V}_{ABC.A_1{B}_1{C}_1}=\frac{1}{12}.\frac{1}{4}V=\frac{1}{48}$

+) $V_3=V_{C.C_{1}NK}=\frac{1}{3}.S_{\Delta C_{1}NK}.C{C}_1=\frac{1}{3}.\frac{1}{4}{S}_{\Delta C_1{B}_1{A}_1}.C{C}_1$

          $=\frac{1}{12}{V}_{ABC.A_1{B}_1{C}_1}=\frac{1}{12}.\frac{1}{4}V=\frac{1}{48}$

+) $V=S_{ABCD}.A^{\text{'}}A=2S_{\Delta BCD}.A^{\text{'}}A=2.\frac{1}{2}.\left(4a\right).\left(4a\right).\sin 120°.\left(6a\right)=48a^3\sqrt{3}$