Trang chủ
Đề thi & kiểm tra
Khác
Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Cho hình nón đỉnh S có chiều cao bằng bán...
Cho hình nón đỉnh S có chiều cao bằng bán kính đáy và bằng 2a. Mặt phẳng (P) đi
Câu hỏi :
Cho hình nón đỉnh S có chiều cao bằng bán kính đáy và bằng 2a. Mặt phẳng (P) đi qua S cắt đường tròn đáy tại A và B sao cho . Khoảng cách từ tâm của đường tròn đáy hình nón đến (P) bằng
Cho hình nón đỉnh S có chiều cao bằng bán kính đáy và bằng 2a. Mặt phẳng (P) đi qua S cắt đường tròn đáy tại A và B sao cho . Khoảng cách từ tâm của đường tròn đáy hình nón đến (P) bằng
A.
B.
C.
D. a
* Đáp án
C
* Hướng dẫn giải
Đáp án C
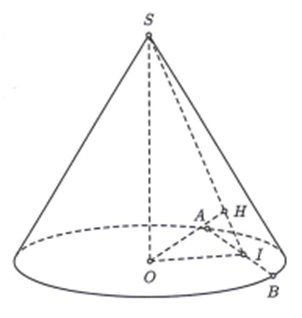
Ta có (P) = (SAB). Gọi O là tâm của đường tròn đáy, I là
trung điểm của AB.
Kẻ
Xét tam giác vuông OIA có:
Xét tam giác SOI vuông tại O, OH là đường cao ta có:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 311
Copyright © 2021 HOCTAP247
