Một mặt cầu có tâm O nằm trên mặt phẳng đáy của hình chóp tam giác đều S.ABC có
Câu hỏi :
Một mặt cầu có tâm O nằm trên mặt phẳng đáy của hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau, các điểm A, B, C thuộc mặt cầu. Biết bán kính mặt cầu là 1. Tính tổng độ dài l các giao tuyến của mặt cầu với các mặt bên của hình chóp thỏa mãn.
Một mặt cầu có tâm O nằm trên mặt phẳng đáy của hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau, các điểm A, B, C thuộc mặt cầu. Biết bán kính mặt cầu là 1. Tính tổng độ dài l các giao tuyến của mặt cầu với các mặt bên của hình chóp thỏa mãn.
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Đáp án C
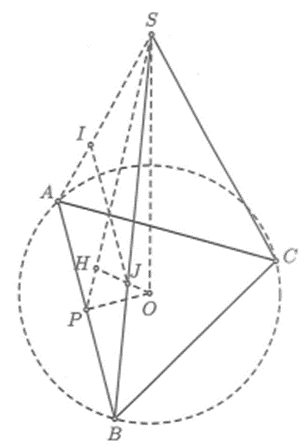
Bán kính mặt cầu . Đặt .
Ta có OA = OB = OC = 1.
Mà tam giác ABC đều nên suy ra .
Từ giả thiết ta có S.ABC là tứ diện đều (P là trung điểm AB)
Ta có tam giác SOP vuông tại O có đường cao OH
và ,
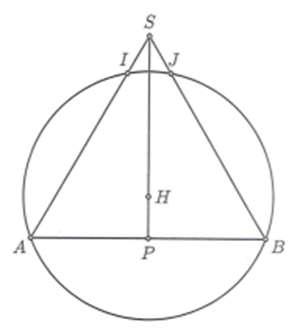
Vì là đường tròn bánh kính
Xét tam giác vuông SOP có:
Xét tam giác vuông HPA có:
Giao tuyến của (S) vói amwjt bên (SAB) là cung IJ.
Góc ngoài đường tròn là
=> độ dài cung IJ:
=> tổng độ dài l các giao tuyến của mặt cầu với các mặt bên của hình chóp là:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Copyright © 2021 HOCTAP247
