Trong không gian Oxyz, cho tam giác ABC nội tiếp đường tròn tâm I(2; 3; -4), trực

Đáp án A

Ta có $\overrightarrow{AI}=\left(1;5;-4\right)$, $\overrightarrow{AH}=\left(2;2;1\right)$ nên $\left[\overrightarrow{AI},\overrightarrow{AH}\right]=\left(13;-9;-8\right)$ là véc tơ pháp tuyến của mặt phẳng $\left(ABC\right)$ suy ra $\left[\overrightarrow{AI},\overrightarrow{AH}\right]$ có giá vuông góc với đường thẳng BC.

Mà $\overrightarrow{AH}$ có giá vuông góc với BC nên véc tơ chỉ phương của đường thẳng BC là

$\overrightarrow{u}=\left[\overrightarrow{AH},\left[\overrightarrow{AI},\overrightarrow{AH}\right]\right]=\left(-7;29;-44\right)$

Gọi A' là điểm đối xứng của A qua I thì A(3; 8; -8).

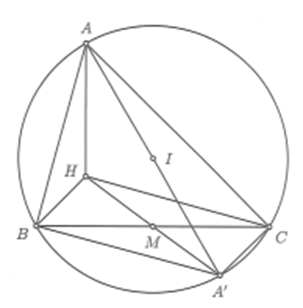
Ta có $\Delta AC{A}^{\text{'}}$ vuông tại C $\Rightarrow A^{\text{'}}C\perp AC$; H là trọng tâm $\Delta ABC\Rightarrow BH\perp AC$.

$\Rightarrow BH//A\text{'}C.$ Tương tự CH//A’B

$\Rightarrow BHC{A}^{\text{'}}$ là hình bình hành => BC đi qua trung điểm $M\left(3;4;-\frac{7}{2}\right)$ của A'H.

Do đó BC có phương trình là: $\frac{x-3}{-7}=\frac{y-4}{29}=\frac{z+\frac{7}{2}}{-44}$