Trang chủ
Đề thi & kiểm tra
Khác
Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Cho hàm số y = f(x) = ax^5 + bx^4...
Cho hàm số y = f(x) = ax^5 + bx^4 + cx^3 + dx^2 + ẽ + f (a khác 0) Biết hàm số y = f'(x) có
Câu hỏi :
Cho hàm số . Biết hàm số y = f'(x) có đồ thị như hình bên. Đặt . Hàm số có bao nhiêu điểm cực trị?
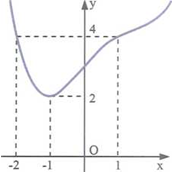
Cho hàm số . Biết hàm số y = f'(x) có đồ thị như hình bên. Đặt . Hàm số có bao nhiêu điểm cực trị?

A. 7
B. 3
C. 9
D. 5
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Ta có .
.
Đặt t = 3x - 1, ta được
Sử dụng tương giao hai đồ thị của hai hàm số y = f'(x) và ta suy ra phương trình có 3 nghiệm đơn t = -2, t = -1, t = 1.
Từ đó suy ra phương trình có 3 nghiệm đơn , x = 0, .
=> y = g(x) có 1 điểm cực trị trên có 3 điểm cực trị.Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 311
Copyright © 2021 HOCTAP247
