Cho tam giác ABC vuông tại A có BC = 2a, căn bậc 2 6/3 AC, Ab theo thứ tự lập thành một cấp

* Hướng dẫn giải

Đáp án D

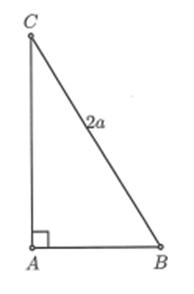
Ta có tam giác ABC vuông tại A có BC = 2a, $\frac{\sqrt{6}}{3}AC$, AB lập thành một cấp số nhân nên suy ra $BC.AB=\frac{2}{3}A{C}^2$.

Theo hệ thức lượng trong tam giác vuông: Ac = BCsinB, AB = ACcosB.

Do đó $BC.AB=\frac{2}{3}A{C}^2$

$$\begin{gathered} \iff 3B{C}^2.\cos B=2B{C}^2.{\sin }^{2}B \\ \iff 2{\cos }^{2}B+3\cos B-2=0 \Rightarrow \cos B=\frac{1}{2}\Rightarrow \widehat{B}=60° \end{gathered}$$

Vậy $AC=BC.\sin 60°=a\sqrt{3}$, AB= a.

Suy ra $\left\{\begin{array}{l}{S}_{\Delta ABC}=\frac{1}{2}AB.AC=\frac{1}{2}{a}^2\sqrt{3}\\ p=\frac{3a+a\sqrt{3}}{2}\end{array}\right.\Rightarrow r=\frac{S}{p}=\frac{\sqrt{3}-1}{2}a$.