Cho N là điểm biểu diễn số phức z thỏa mãn (z + 2 - 3i)/(z - 3) = 1- i và M là điểm

+) Ta có $\frac{z+2-3i}{z-3}=1-i\iff z+2-3i=\left(1-i\right)z-3+3i\iff iz=-5+6i$

$\iff z=\frac{-5+6i}{i}=6+5i$. Suy ra N(6; 5).

+) Gọi A(2; 1), B(-3; 3) $\Rightarrow AB=\sqrt{25+4}=\sqrt{29}$.

M(x; y) là điểm biểu diễn của số phức z' thỏa mãn $\left|z^{\text{'}}-2-i\right|+\left|z^{\text{'}}+3-3i\right|=\sqrt{29}$.

Ta thấy $\left|z^{\text{'}}-2-i\right|+\left|z^{\text{'}}+3-3i\right|=\sqrt{29}\iff MA+MB=AB$. Suy ra quỹ tích điểm M là đoạn thẳng AB.

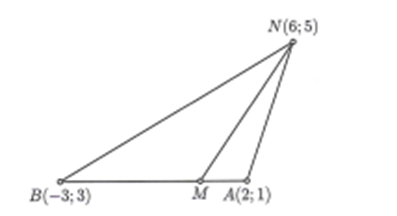
+) $\overrightarrow{AN}\left(4;4\right)$, $\overrightarrow{AB}\left(-5;2\right)$ $\Rightarrow \overrightarrow{AN}.\overrightarrow{AB}=-20+8=-12<0$. Suy ra tam giác NAB là tam giác tù tại A.

Khi đó, M thuộc đoạn thẳng AB thì MN nhỏ nhất khi và chỉ khi M trùng A.

Vậy giá trị nhỏ nhất của MN là $AN=\sqrt{16+16}=4\sqrt{2}$.