Biết số phức z thỏa mãn 2}z - 1| < = |z - z (có gạch trên đầu) - 3i| và z - z (có gạch trên đầu)

* Hướng dẫn giải

Đáp án D

Gọi $z=x+yi\left(x,y\in ℝ\right)$.

Ta có:$2\left|z-i\right|\le \left|z-\overline{z}-3i\right|\iff 2\sqrt{x^2+{\left(y-1\right)}^2}\le \sqrt{{\left(2y-3\right)}^2}$

$\iff 4x^2+4y^2-8y+4\le 4y^2-12y+9\iff 4y\le -4x^2+5\iff y\le -x^2+\frac{5}{4}\left(1\right)$

Số phức $z-\overline{z}=2yi$ có phần ảo không âm $\iff y\ge 0\left(2\right)$.

Từ (1) và (2) ta suy ra phần mặt phẳng chứa các điểm biểu diễn cho số phức z là hình phẳng giới hạn bởi Parabol $\left(P\right):y=-x^2+\frac{5}{4}$ và trục hoành.

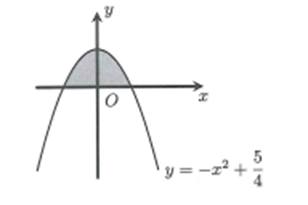
Phương trình hoành độ giao điểm của (P) và trục hoành là: $-x^2+\frac{5}{4}=0\iff x=\pm \frac{\sqrt{5}}{2}$.

Gọi S là diện tích cần tìm $\Rightarrow S=2\underset{0}{\overset{\frac{\sqrt{5}}{2}}{\int }}\left(-x^2+\frac{5}{4}\right)dx={\left.2\left(-\frac{x^3}{3}+\frac{5}{4}x\right)\right|}_0^{\frac{\sqrt{5}}{2}}=\frac{5\sqrt{5}}{6}$.