Cho hình chóp S.ABCD có ABCD là hình chữ nhật tâm I cạnh AB = 3a; BC = 4a. Hình

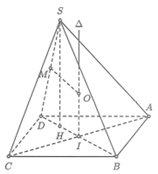
Gọi H là trung điểm của $ID\Rightarrow SH\perp \left(ABCD\right)$ 

Trong mặt phẳng (SBD), qua I dựng đường thẳng $\Delta$ song song với SH. Suy ra  là trục đường tròn ngoại tiếp ABCD. Gọi M là trung điểm của SD.

Trong mặt phẳng (SBD), dựng đường trung trực của đoạn thẳng SD, cắt  tại O. Suy ra SO = OD.

Mà OA = OB = OC = OD nên O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.

Ta có ABCD là hình chữ nhật tâm I cạnh AB = 3a; BC = 4a. và H là trung điểm DI.

Nên suy ra $DI=\frac{5a}{2};BH=\frac{15a}{4};HI=\frac{5a}{4}$.

Ta có $\left(SB;\left(ABCD\right)\right)=\widehat{SBH}={45}^o$

Xét tam giác SHB vuông ại H có $\widehat{SHB}={45}^o$

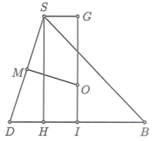
Từ S dựng đường thẳng song song với BD, cắt $\Delta$ tại G.

=> SHIG là hình chữ nhật $\Rightarrow GI=\frac{15a}{4};SG=HI=\frac{5a}{4}$

Đặt OI = x. Ta có: $R^2=O{D}^2=O{I}^2+D{I}^2=\frac{25a^2}{4}+x^2\left(1\right)$

Lại có: $GO=GI-OI=\frac{15a}{4}-x$

Mà $R^2=S{O}^2=S{G}^2+G{O}^2=\frac{25a^2}{16}+{\left(\frac{15a}{4}-x\right)}^2\left(2\right)$

Từ (1) và (2) => $\frac{25a^2}{4}+x^2=\frac{25a^2}{16}+{\left(\frac{15a}{4}-x\right)}^2\iff x=\frac{5a}{4}$

Vậy bán kính mặt cầu ngoại tiếp hình chóp là $R=\sqrt{\frac{25a^2}{4}+{\left(\frac{5a}{4}\right)}^2}=\frac{5\sqrt{5}}{4}a$

Suy ra diện tích mặt cầu cần tính là $S=4\pi R^2=\frac{125\pi }{4}{a}^2$