Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S1): (x - 1)^2 + (y - 1)^2 + (z - 2)^2 = 16

Câu hỏi :

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu $\left(S_1\right):{\left(x-1\right)}^2+{\left(y-1\right)}^2+{\left(z-2\right)}^2=16$ và $\left(S_2\right):{\left(x+1\right)}^2+{\left(y-2\right)}^2+{\left(z+1\right)}^2=9$  cắt nhau theo giao tuyến là đường tròn (C). Tìm tọa độ tâm J của đường tròn (C)

* Đáp án

B

* Hướng dẫn giải

Đáp án B

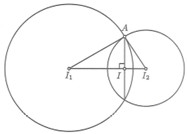
Ta có (S₁) và (S₂) có tâm và bán kính lần lượt là $I_1\left(1;1;2\right),R_1=4$ và $I_2\left(-1;2;-1\right),R_2=3$ 

$\Rightarrow \overrightarrow{I_1{I}_2}=\left(-2;1;-3\right)\Rightarrow I_1{I}_2=\sqrt{14}$

Gọi I(x; y; z) là tâm của đường tròn giao tuyến (C) và A là một điểm thuộc (C).

Ta có:

 $$\begin{gathered} I_{1}I=I_{1}A.\cos \widehat{A{I}_{1}I}=R_1.\cos \widehat{A{I}_1{I}_2}=R_1.\frac{I_1{A}^2+I_1{I}_2^2-A{I}_2^2}{2.I_{1}A.I_1{I}_2}=4.\frac{4^2+\sqrt{{14}^2}-3^2}{\mathrm{2.4.}\sqrt{14}}=\frac{21}{2\sqrt{14}} \\ \overrightarrow{I_{1}I}=\frac{\left|\overrightarrow{I_{1}I}\right|}{\left|\overrightarrow{I_1{I}_2}\right|}\overrightarrow{I_1{I}_2}\iff \overrightarrow{I_{1}I}=\frac{\frac{21}{2\sqrt{14}}}{\sqrt{14}}\overrightarrow{I_1{I}_2}\iff \overrightarrow{I_{1}I}=\frac{3}{4}\overrightarrow{I_1{I}_2}\iff \left\{\begin{array}{l}x-1=\frac{3}{4}.\left(-2\right)\\ y-1=\frac{3}{4}.1\\ z-2=\frac{3}{4}.\left(-3\right)\end{array}\right.\iff \left\{\begin{array}{l}x=-\frac{1}{2}\\ y=\frac{7}{4}\\ z=-\frac{1}{4}\end{array}\right. \end{gathered}$$