hãy tính theo a khoảng cách d từ M đến mặt phẳng (SAC)

Đáp án

Phương pháp giải: - Đổi $d\left(M;\left(SAC\right)\right)$ sang $d\left(H;\left(SAC\right)\right)$.

- Trong $\left(ABCD\right)$ kẻ $HE\perp AC\left(E\in AC\right)$, trong $\left(SHE\right)$ kẻ $HN\perp SE\left(N\in SE\right)$, chứng minh $HN\perp \left(SAC\right)$

- Xác định góc giữa SC và , từ đó tính $SH$.

- Sử dụng $S_{HAC}=\frac{1}{2}HE.AC=\frac{1}{2}{S}_{ABC}$, từ đó tính $HE$.

- Sử dụng hệ thức lượng trong tam giác vuông tính $HN$.

Giải chi tiết:

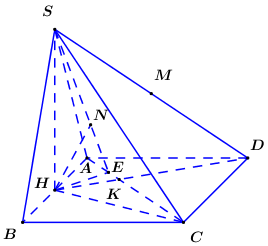
Gọi H là trung điểm $AB$. Vì $\Delta SAB$ cân tại S nên $SH\perp AB$.

Ta có: $\left\{\begin{array}{l}\left(SAB\right)\cap \left(ABCD\right)=AB\\ SH\subset \left(ABCD\right),SH\perp AB\end{array}\right.$ $\Rightarrow SH\perp \left(ABCD\right)$.

Gọi $K=HD\cap AC$. Áp dụng định lí T-aet ta có $\frac{DK}{HK}=\frac{DC}{AH}=2\Rightarrow DK=2HK$.

Ta có $MD\cap \left(SAC\right)=S\Rightarrow \frac{d\left(M;\left(SAC\right)\right)}{d\left(D;\left(SAC\right)\right)}=\frac{SM}{SD}=\frac{1}{2}$

$\Rightarrow d\left(M;\left(SAC\right)\right)=\frac{1}{2}d\left(D;\left(SAC\right)\right)$.

Lại có $DH\cap \left(SAC\right)=K$ nên $\frac{d\left(D;\left(SAC\right)\right)}{d\left(H;\left(SAC\right)\right)}=\frac{DK}{HK}=2\Rightarrow d\left(D;\left(SAC\right)\right)=2d\left(H;\left(SAC\right)\right)$.

Do đó $d\left(M;\left(SAC\right)\right)=d\left(H;\left(SAC\right)\right)$

Trong $\left(ABCD\right)$ kẻ $HE\perp AC\left(E\in AC\right)$, trong $\left(SHE\right)$ kẻ $HN\perp SE\left(N\in SE\right)$ ta có:

$\left\{\begin{array}{l}AC\perp HE\\ AC\perp SH\end{array}\right.\Rightarrow AC\perp \left(SHE\right)\Rightarrow AC\perp HN$

$\left\{\begin{array}{l}HN\perp SE\\ HN\perp AC\end{array}\right.\Rightarrow HN\perp \left(SAC\right)\Rightarrow d\left(H;\left(SAC\right)\right)=HN$

Vì $SH\perp \left(ABCD\right)$ nên $HC$ là hình chiếu vuông góc của $SC$ lên $\left(ABCD\right)$.

$\Rightarrow \angle \left(SC;\left(ABCD\right)\right)=\angle \left(SC;HC\right)=\angle SCH={45}^0$

$\Rightarrow \Delta SHC$ vuông cân tại H $\Rightarrow SH=HC=\sqrt{B{C}^2+B{H}^2}=\sqrt{{\left(2a\right)}^2+{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{17}}{2}$.

Ta có: $S_{HAC}=\frac{1}{2}HE.AC=\frac{1}{2}{S}_{ABC}$

$\Rightarrow HE.AC=\frac{1}{2}.AB.BC\Rightarrow HE=\frac{\frac{1}{2}.AB.BC}{AC}=\frac{\frac{1}{2}.a.2a}{\sqrt{a^2+{\left(2a\right)}^2}}=\frac{a}{\sqrt{5}}$

Áp dụng hệ thức lượng trong tam giác vuông $SHE$ ta có:

Nên $HN=\frac{SH.HE}{\sqrt{S{H}^2+H{E}^2}}=\frac{\frac{a\sqrt{17}}{2}.\frac{a}{\sqrt{5}}}{\sqrt{\frac{17a^2}{4}+\frac{a^2}{5}}}=\frac{a\sqrt{1513}}{89}$

Vậy $d\left(M;\left(SAC\right)\right)=\frac{a\sqrt{1513}}{89}$.