Tìm các giá trị thực của tham số m để phương trình có bốn nghiệm thực phân biệt.

* Hướng dẫn giải

Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số

\[y = \left| {{x^2} - 3x + 2} \right|\]với đường thẳng y = m có tính chất song song với trục hoành.

Ta có \[y = \mid {x^2} - 3x + 2\mid = \left\{ {\begin{array}{*{20}{c}}{{x^2} - 3x + 2({x^2} - 3x + 2 \ge 0)}\\{ - {x^2} + 3x - 2({x^2} - 3x + 2 < 0)}\end{array}} \right.\]

Đồ thị hàm số \[y = \left| {{x^2} - 3x + 2} \right|\]được vẽ như sau:

+ Vẽ đồ thị hàm số \[y = {x^2} - 3x + 2\]+ Lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa phần đồ thị dưới trục hoành đi.

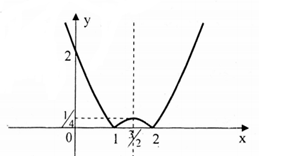
Dựa trên đồ thị ta thấy phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi \[0 < m < \frac{1}{4}\]

Đáp án cần chọn là: B