Tìm các giá trị của tham số m để phương trình có 3 nghiệm thực phân biệt.

* Hướng dẫn giải

Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số

\[y = \frac{1}{2}{x^2} - 4\left| x \right| + 3 = \left\{ {\begin{array}{*{20}{c}}{\frac{1}{2}{x^2} - 4x + 3(x \ge 0)}\\{\frac{1}{2}{x^2} + 4x + 3(x < 0)}\end{array}} \right.\]và đường thẳng \[y = {m^2}\]có tính chất song song với trục hoành.

Đồ thị hàm số \[y = \frac{1}{2}{x^2} - 4\left| x \right| + 3\]được vẽ như sau :

+ Vẽ hai đồ thị hàm số trên cùng một hệ trục tọa độ.

+ Giữ nguyên nhánh bên phải trục tung của đồ thị hàm \[y = \frac{1}{2}{x^2} - 4x + 3\] và xóa nhánh bên trái trục tung.

+ Giữ nguyên nhánh bên trái trục tung của đồ thị hàm số \[y = \frac{1}{2}{x^2} + 4x + 3\] và xóa nhánh bên phải trục tung của đồ thị hàm số đó.

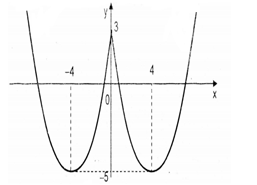
Dựa trên đồ thị ta thấy phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi

\[{m^2} = 3 \Leftrightarrow m = \pm \sqrt 3 \]

Đáp án cần chọn là: C