Tìm các giá trị của tham số mm để phương trình có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1).

* Hướng dẫn giải

Có: \[{\rm{\Delta '}} = {\left( {m + 1} \right)^2} - 1 = m\left( {m + 2} \right)\]

Phương trình có hai nghiệm phân biệt ⇔\[m(m + 2) >0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m >0}\\{m < - 2}\end{array}} \right.\]Khi đó dạng đồ thị hàm số \[y = {x^2} - 2\left( {m + 1} \right)x + 1\] chỉ có thể là:

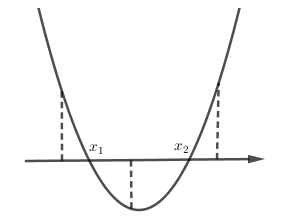
Quan sát đồ thị ta thấy:  

Yêu cầu bài toán tương đương \[f\left( 0 \right).f\left( 1 \right) < 0 \Leftrightarrow 1.\left( { - 2m} \right) < 0 \Leftrightarrow m >0\]</>

Kết hợp điều kiện có hai nghiệm phân biệt ta được m >0

Đáp án cần chọn là: A