Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2020 để phương trình

* Hướng dẫn giải

Chọn D

Phương trình đã cho tương đương với phương trình

$m+\sqrt{m+2^x}=2^{2x}\iff \left(m+2^x\right)+\sqrt{m+2^x}=2^{2x}+2^x$(1)

Ta có $\sqrt{m+2^x}\ge 0$, $2^x>0$.

Xét hàm đặc trưng $f\left(t\right)=t^2+t$ trên $\left[0;+\infty \right)$.

Ta có $f^{\text{'}}\left(t\right)=2t+1\ge 0$, $\forall t\in \left[0;+\infty \right)$ 

$\Rightarrow f\left(t\right)$ đồng biến trên khoảng $\left[0;+\infty \right)$.

Do đó$\left(1\right)\iff f\left(\sqrt{m+2^x}\right)=f\left(2^x\right)\iff \sqrt{m+2^x}=2^x\iff m=2^{2x}-2^x\left(2\right)$.

Đặt $a=2^x$, $a>0$. Ta có $\left(2\right)\iff m=g\left(a\right)=a^2-a$

 

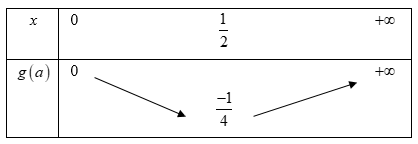
Phương trình đã cho có nghiệm $\iff m\ge -\frac{1}{4}$ mà m là giá trị nguyên dương nhỏ hơn 2020 nên $m\in \left\{1;2;3;\mathrm{...};2019\right\}$.

Vậy có 2019 giá trị m thỏa mãn yêu cầu bài toán.