Cho hình lăng trụ đều ABC.A’B’C’ có độ dài tất cả các cạnh bằng a.

* Hướng dẫn giải

Cách 1.

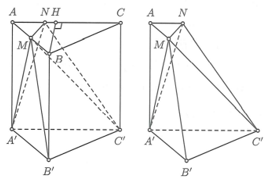
 Gọi V là thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’.

Khi đó ta có $V=V_{M.A\text{'}AN}+V_{M.A\text{'}C\text{'}N}+V_{M.A\text{'}B\text{'}C\text{'}}$ 

Từ giả thiết ta có

$S_{\Delta A\text{'}AN}=\frac{1}{2}AA\text{'}.AN=\frac{1}{2}.a.\frac{a}{3}=\frac{a^2}{6};S_{\Delta A\text{'}C\text{'}N}=\frac{1}{2}d\left(N,A\text{'}C\text{'}\right).A\text{'}C\text{'}=\frac{1}{2}.a.a=\frac{a^2}{2};$ 

$S_{\Delta A\text{'}B\text{'}C\text{'}}=\frac{1}{2}A\text{'}B\text{'}.A\text{'}C\text{'}.sin{60}^o=\frac{a^2\sqrt{3}}{4}$ 

Gọi H là trung điểm của $AC\Rightarrow BH\perp \left(ACC\text{'}A\text{'}\right)$ và $BH=\frac{a\sqrt{3}}{2}$ 

$\Rightarrow d\left(M,\left(ACC\text{'}A\text{'}\right)\right)=\frac{1}{2}d\left(B,\left(ACC\text{'}A\text{'}\right)\right)=\frac{1}{2}BH=\frac{a\sqrt{3}}{4}.$ 

Khi đó ta có

$V_{M.A\text{'}AN}=\frac{1}{3}d\left(M;\left(ACC\text{'}A\text{'}\right)\right).S_{\Delta A\text{'}AN}=\frac{1}{3}.\frac{a\sqrt{3}}{4}.\frac{a^2}{6}=\frac{a^3\sqrt{3}}{72}.$

$\begin{array}{l}{V}_{M.A\text{'}C\text{'}N}=\frac{1}{3}d\left(M,\left(ACC\text{'}A\text{'}\right)\right).S_{\Delta A\text{'}C\text{'}N}=\frac{1}{3}.\frac{a\sqrt{3}}{4}.\frac{a^2}{2}=\frac{a^3\sqrt{3}}{24}.\\ V_{M.A\text{'}B\text{'}C\text{'}}=\frac{1}{3}d\left(M,\left(A\text{'}B\text{'}C\text{'}\right)\right).S_{\Delta A\text{'}B\text{'}C\text{'}}=\frac{1}{3}.a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{12}.\end{array}$ Vậy   $V=V_{M.A\text{'}AN}+V_{M.A\text{'}C\text{'}N}+V_{M.A\text{'}B\text{'}C\text{'}}=\frac{a^3\sqrt{3}}{72}+\frac{a^3\sqrt{3}}{24}+\frac{a^3\sqrt{3}}{12}=\frac{5\sqrt{3}{a}^3}{36}$

Cách 2.

Gọi V là thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’. Khi đó ta có

$V=V_{M.AA\text{'}C\text{'}N}+V_{M.A\text{'}B\text{'}C\text{'}}$ .

Ta có $S_{AA\text{'}C\text{'}N}=\frac{1}{2}AA\text{'}\left(AN+A\text{'}C\text{'}\right)=\frac{1}{2}a\left(\frac{a}{3}+a\right)=\frac{2a^2}{3}.$ 

Suy ra $V_{M.AA\text{'}C\text{'}N}=\frac{1}{3}d\left(M,\left(ACC\text{'}A\text{'}\right)\right).S_{AA\text{'}C\text{'}N}=\frac{1}{3}.\frac{a\sqrt{3}}{4}.\frac{2a^3}{3}=\frac{2\sqrt{3}{a}^3}{36}$ 

$V_{M.A\text{'}B\text{'}C\text{'}}=\frac{1}{3}d\left(M,\left(A\text{'}B\text{'}C\text{'}\right)\right).S_{\Delta A\text{'}B\text{'}C\text{'}}=\frac{1}{3}.a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{12}.$ 

Vậy $V=V_{M.AA\text{'}C\text{'}N}+V_{M.A\text{'}B\text{'}C\text{'}}=\frac{2\sqrt{3}{a}^3}{36}+\frac{a^3\sqrt{3}}{12}=\frac{5\sqrt{3}{a}^3}{36}.$

Cách 3.

Gọi H là trung điểm của AC và V là thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’.

Khi đó, $V=V_{AMH.A\text{'}B\text{'}C\text{'}}-V_{M.NHC\text{'}}$ 

Dễ thấy $MH//B\text{'}C\text{'}$ nên AMH.A’B’C’ là khối chóp cụt.

Áp dụng công thức thể tích V₁ của khối chóp cụt có chiều cao h, diện tích đáy nhỏ và đáy lớn theo thứ tự là S₀, S₁ thì ta có

$V_1=\frac{h}{3}\left(S_0+\sqrt{S_0{S}_1}+S_1\right)$ 

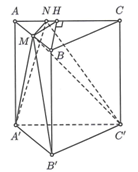
Khi đó

$V_{AMH.A\text{'}B\text{'}C\text{'}}=\frac{AA\text{'}}{3}\left(S_{AMH}+\sqrt{S_{AMH}.S_{A\text{'}B\text{'}C\text{'}}}+S_{A\text{'}B\text{'}C\text{'}}\right)$ 

$=\frac{a}{3}\left(\frac{1}{4}.\frac{a^2\sqrt{3}}{4}+\sqrt{\frac{1}{4}.\frac{a^2\sqrt{3}}{4}.\frac{a^2\sqrt{3}}{4}}+\frac{a^2\sqrt{3}}{4}\right)=\frac{7a^3\sqrt{3}}{48}$ 

Mặt khác, $V_{M.NHC\text{'}}=\frac{1}{3}d\left(M,\left(ACC\text{'}A\text{'}\right)\right).S_{NHC\text{'}}=\frac{1}{3}.\frac{a\sqrt{3}}{4}.\frac{1}{2}.a.\frac{a}{6}=\frac{a^3\sqrt{3}}{144}$ 

Vậy $V=V_{AMH.A\text{'}B\text{'}C\text{'}}-V_{M.NHC\text{'}.}=\frac{7a^3\sqrt{3}}{48}-\frac{a^3\sqrt{3}}{144}=\frac{5\sqrt{3}{a}^3}{36}$ 

Chọn C