Trang chủ
Đề thi & kiểm tra
Khác
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Cho tứ diện ABCD có góc ABC = góc ADC...
Cho tứ diện ABCD có góc ABC = góc ADC =góc BCD =90 độ, BC=2a, CD=a,
Câu hỏi :
Cho tứ diện ABCD có , góc giữa đường thẳng AB và mặt phẳng (BCD) bằng . Tính khoảng cách giữa hai đường thẳng AC và BD
Cho tứ diện ABCD có , góc giữa đường thẳng AB và mặt phẳng (BCD) bằng . Tính khoảng cách giữa hai đường thẳng AC và BD
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
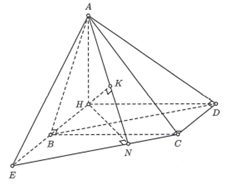
Gọi H là hình chiếu vuông góc của A lên mặt phẳng (BCD).
Do
Tương tự
Ta có
Từ (1), (2), (3) nên tứ giác là hình chữ nhật HBCD có và .
Gọi E là đỉnh của hình bình hành BDCE. Khoảng cách giữa hai đường thẳng AC và BD bằng Gọi HN là đường cao tam giác HEC, HK là đường cao tam giác AHN.
Ta có
và nên
Vậy
Trong có
Trong có
Vậy
Chọn C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 300
Copyright © 2021 HOCTAP247
