Trang chủ
Đề thi & kiểm tra
Khác
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Cho tứ diện ABCD có góc DAB= góc CBD =90...
Cho tứ diện ABCD có góc DAB= góc CBD =90 độ; AC=a* căn bậc hai của 5; góc ABC =135 độ .
Câu hỏi :
Cho tứ diện ABCD có . Biết góc giữa hai mặt phẳng (ABD),(BCD) bằng . Thể tích của tứ diện ABCD bằng
A.
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
Dựng .
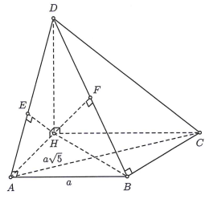
Ta có .
Tương tự
Tam giác AHB có
vuông cân tại .
Áp dụng định lý cosin, ta có .
Vậy .
Dựng và .
Suy ra và tam giác HEF vuông tại E.
Đặt , khi đó .
Suy ra
Vậy .
Chọn D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 300
Copyright © 2021 HOCTAP247
