Cho hình chóp S.ABCD có đáy là hình chữ nhật,

Câu hỏi :

Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết $AB=2a,AD=a,SA=3a$  và SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh CD, điểm $E\in SA$  sao cho SE=a, cosin của góc giữa hai mặt phẳng (SAC) và (BME) bằng

* Đáp án

* Hướng dẫn giải

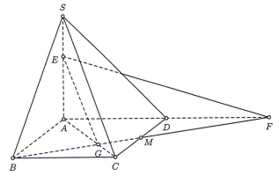
Góc giữa hai mặt phẳng $\left(\alpha \right)$ và $\left(\beta \right)$ là góc $\phi$. Khi đó $\sin \phi =\frac{d\left(A,\alpha \right)}{d\left(A,\Delta \right)}$. Gọi điểm G là trọng tâm $\Delta BCD$, kéo dài tia BM cắt AD tại F.

Ta có $\left(SAC\right)\cap \left(BEF\right)=EG$.

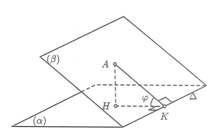
Khi đó góc giữa hai mặt phẳng (SAC) và (BME) là góc $\phi$ có $\sin \phi =\frac{d\left(A,\left(BEF\right)\right)}{d\left(A,EG\right)}$.

Ta có $d\left(A,\left(BEF\right)\right)=\frac{2a\sqrt{3}}{3},d\left(A,EG\right)=\frac{AE.AG}{\sqrt{A{E}^2+A{G}^2}}=\frac{a\sqrt{70}}{7}$

$\Rightarrow \sin \phi =\frac{d\left(A,\left(BEF\right)\right)}{d\left(A,EG\right)}=\frac{\sqrt{14}}{\sqrt{15}}\Rightarrow \cos \phi =\frac{1}{\sqrt{15}}$.