Trang chủ
Đề thi & kiểm tra
Khác
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Cho hình chóp S.ABCD có cạnh SA = x còn...
Cho hình chóp S.ABCD có cạnh SA = x còn tất cả các cạnh khác có độ dài bằng 2.
Câu hỏi :
Cho hình chóp S.ABCD có cạnh SA = x còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích V lớn nhất của khối chóp S.ABCD.
Cho hình chóp S.ABCD có cạnh SA = x còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích V lớn nhất của khối chóp S.ABCD.
A. V=1
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
Gọi O là giao điểm của AC và BD.
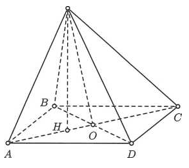
Ta có nên
vuông tại S.
Do đó,
.
Ta thấy .
Trong hạ .
Khi đó, .
Xét tam giác vuông SAC có
.
Dấu “=” xảy ra khi và chỉ khi .
Chọn D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 300
Copyright © 2021 HOCTAP247
