Trang chủ
Đề thi & kiểm tra
Khác
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Cho hai số phức z1, z2 thỏa mãn |z1|=2, |z2|=...
Cho hai số phức z1, z2 thỏa mãn |z1|=2, |z2|= căn bậc hai của 3.
Câu hỏi :
Cho hai số phức thỏa mãn , . Gọi M, N là các điểm biểu diễn cho và . Biết . Tính .
Cho hai số phức thỏa mãn , . Gọi M, N là các điểm biểu diễn cho và . Biết . Tính .
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
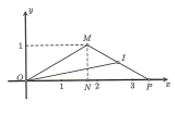
Ta có
Gọi P là điểm biểu diễn của số phức .
Khi đó ta có
(I là trung điểm PM).
Do nên áp dụng định lí cosin ta tính được MN = 1.
Khi đó có MN đồng thời là đường cao và đường trung tuyến,
suy ra cân tại M .
Áp dụng định lí đường trung tuyến cho ta có: .
Vậy .
Chọn C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2022 có đáp án !!
Số câu hỏi: 300
Copyright © 2021 HOCTAP247
