Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V.

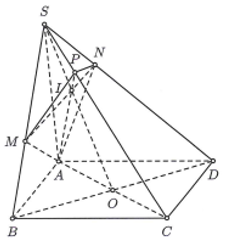
Công thức giải nhanh (chỉ áp dụng với hình chóp có đáy là hình bình hành). Hình chóp SABCD  có$\frac{SM}{SA}=a;\frac{SN}{SB}=b;\frac{SP}{SC}=c;\frac{SQ}{SD}=d.$

 Khi đó,

 $\frac{1}{a}+\frac{1}{c}=\frac{1}{b}+\frac{1}{d}\Rightarrow \frac{V_{SMNPQ}}{V_{SABCD}}=\frac{abcd}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right).$

Áp dụng công thức giải nhanh vào bài toán:

+) Đặt$a=\frac{SA}{SA}=1;b=\frac{SB}{SM};c=\frac{SC}{SP}=5;d=\frac{SD}{SN}.$

+) Ta có$a+c=b+d\iff 1+5=b+d\iff d=6-b.$

+)$\frac{V_{S.AMPN}}{V_{S.ABCD}}=\frac{a+b+c+d}{4abcd}=\frac{1+b+5+6-b}{\mathrm{4.1.}b\mathrm{.5.}\left(6-b\right)}=\frac{3}{5}.\frac{1}{-b^2+6b}.$

+) Xét  $f\left(b\right)=\frac{3}{5}.\frac{1}{-b^2+6b};b\in \left[1;5\right].$

$f^{\text{'}}\left(b\right)=-\frac{3}{5}.\frac{-2b+6}{{(-b^2+6b)}^2};$$f\text{'}\left(b\right)=0\iff b=3.$

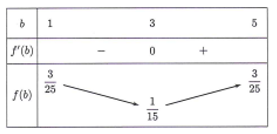
Từ bảng biến thiên (hình bên) ta có giá trị lớn nhất của $\frac{V_1}{V}=\frac{3}{25}$ .

Chọn C