Cho hai đường tròn (O1;10) và (O2;8) cắt nhau tại hai điểm A, B

Câu hỏi :

Cho hai đường tròn $\left(O_1;10\right)$  và $\left(O_2;8\right)$  cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn . Gọi (H) là hình phẳng giới hạn bởi hai đường tròn (phần tô đậm). Quay (H) quanh trục $O_1{O}_2$  ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay tạo thành.

* Đáp án

B

* Hướng dẫn giải

Ta xây dựng hệ trục Oxy tọa độ như hình vẽ

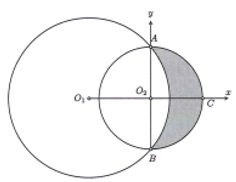
Ta có $O_2\left(0;0\right),O_1\left(-6;0\right),C\left(8;0\right).$

Ta có $O_1{O}_2=\sqrt{O_1{A}^2-O_2{A}^2}=6.$

Đường tròn  có phương trình là $x^2+y^2=64\iff y=\sqrt{64-x^2}\left(-8\le x\le 8\right).$

Đường tròn $\left(O_1;10\right)$ có phương trình là ${\left(x+6\right)}^2+y^2=100$

$\Rightarrow y=\sqrt{100-{\left(x+6\right)}^2}\left(-16\le x\le 4\right).$

Thể tích cần tìm $V=\pi \underset{0}{\overset{8}{\int }}\left(64-x^2\right)dx-\pi \underset{0}{\overset{4}{\int }}\left[100-{\left(x+6\right)}^2\right]dx=\frac{608\pi }{3}.$

Chọn B