Trong không gian với hệ tọa độ Oxy, cho tứ diện ABCD có

* Hướng dẫn giải

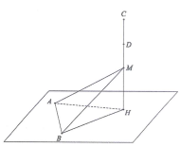
Gọi $C_{ABM}$  là chu vi của tam giác ABM.

$\overrightarrow{AB}=\left(-2;-3;-10\right)\Rightarrow AB=\sqrt{113}$

$\overrightarrow{AB}=\left(-2;-3;-10\right),\overrightarrow{CD}=\left(1;-4;1\right)\Rightarrow \overrightarrow{AB}.\overrightarrow{CD}=-2+12-10=0\Rightarrow AB\perp CD$Gọi (P) là mặt phẳng chứa đường thẳng AB và vuông góc với đường thẳng CD; H là giao điểm của (P) và đường thẳng CD.

Phương trình mặt phẳng (P) đi qua $A\left(-1;1;6\right)$  có vectơ pháp tuyến $\overrightarrow{CD}=\left(1;-4;1\right)$   là: $x-4y+z-1=0$ .

Phương trình đường thẳng $CD:\left\{\begin{array}{l}x=1+t\\ y=2-4t\\ z=-1+t\end{array}\right.$ .

Vì $H\in CD$  nên $H\left(1+t;2-4t;-1+t\right)$ .

Mà $H\in \left(P\right)\iff 1+t-4\left(2-4t\right)-1+t-1=0\iff t=\frac{1}{2}\iff H\left(\frac{3}{2};0;-\frac{1}{2}\right)$ .

Với $\forall M\in CD$ , ta có $\left\{\begin{array}{l}AM\ge AH\\ BM\ge BH\end{array}\right.\Rightarrow AM+BM\ge AH+BH$ .

$C_{ABM}=AB+AM+BM\ge \sqrt{113}+AH+BH,\forall M\in CD$

Suy ra $\min C_{ABM}=\sqrt{113}+AH+BH$ , đạt được $M\equiv H\iff M\left(\frac{3}{2};0;-\frac{1}{2}\right)$ .

Vậy $a+b+c=1$ .

Chọn A