Trong không gian Oxyz, cho (P) x+2y-2z+5=0 và 2 mặt cầu (S1): (x-2)^2 +y^2 +(z+1)^2=1

* Hướng dẫn giải

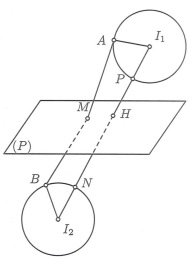
Mặt phẳng (P) có một vectơ pháp tuyến là $\overrightarrow{n_P}=\left(1;2;-2\right)$ .

Mặt cầu $\left(S_1\right)$  có tâm $I_1\left(2;0;-1\right)$  và bán kính $R_1=1$ .

Mặt cầu $\left(S_2\right)$  có tâm $I_2\left(-4;-2;3\right)$  và bán kính $R_2=2$.

Ta có $\overrightarrow{I_1{I}_2}=\left(-6;-2;4\right)\Rightarrow I_1{I}_2=2\sqrt{14}>R_1+R_2$  suy ra $\left(S_1\right)$ ,$\left(S_2\right)$ nằm ngoài nhau.

Ta có $\left(x_{I_1}+2y_{I_1}-2z_{I_1}+5\right)\left(x_{I_2}+2y_{I_2}-2z_{I_2}+5\right)<0$  nên  nằm về hai phía đối với mặt phẳng (P). Ngoài ra

$d\left[I_1,\left(P\right)\right]=3>R_1,d\left[I_2,\left(P\right)\right]=3>R_2$

Gọi N, P, H lần lượt là giao điểm của đoạn thẳng $I_1{I}_2$  với hai mặt cầu $\left(S_1\right)$ , $\left(S_2\right)$và . Ta có

$MA+MB+A{I}_1+B{I}_2\ge I_1{I}_2$

$\iff MA+MB+N{I}_1+P{I}_2\ge I_{1}N+NP+P{I}_2\iff MA+MB\ge NP$

Đẳng thức xảy ra khi và chỉ khi $A\equiv N,B\equiv P$ và $M\equiv H$ .

Khi đó, ${\left(MA+MB\right)}_{\min }=NP=I_1{I}_2-R_1-R_2=2\sqrt{14}-3$.

Chọn B