Cho tứ diện ABCD. Gọi

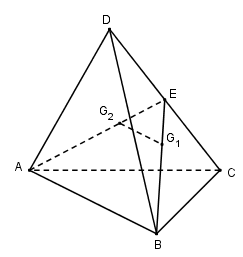
Gọi E là trung điểm của\[CD \Rightarrow {G_1} \in BE;{G_2} \in AE \Rightarrow B{G_1};A{G_2};CD\] đồng quy tại E. Suy ra C đúng.

Ta có:\[\frac{{E{G_1}}}{{EB}} = \frac{{E{G_2}}}{{EA}} = \frac{1}{3} \Rightarrow {G_1}{G_2}//AB\] và \[{G_1}{G_2} = \frac{1}{3}AB\] (Định lí Ta-let đảo)

Mà \[AB \subset \left( {ABD} \right) \Rightarrow {G_1}{G_2}//(ABD)\]

\[AB \subset \left( {ABC} \right) \Rightarrow {G_1}{G_2}//(ABC).\]

Suy ra A và B đúng. Vậy D sai