Cho hình chóp S.ABC, M là một điểm nằm trong tam giác ABC. Các đường thẳng qua MM và song song với SA,SB,SC cắt các mặt (SBC),(SAC),(SAB) lần lượt tại A′,B′,C′.

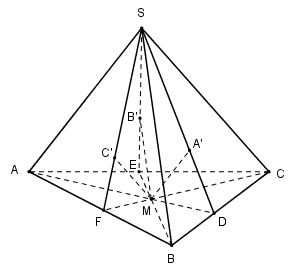
Trong (SAD) ta kẻ đường thẳng qua M và song song với SA cắt (SBC) tại A′.A′.

Trong (SCF) kẻ đường thẳng qua M và song song với SC cắt SF tại C′

\[MA'//SA \Rightarrow \frac{{MA'}}{{SA}} = \frac{{DM}}{{DA}} = \frac{{{S_{MBC}}}}{{{S_{ABC}}}}\]

Tương tự ta chứng minh được \[\frac{{MB'}}{{SB}} = \frac{{EM}}{{EB}} = \frac{{{S_{MAC}}}}{{{S_{ABC}}}}\] và\[\frac{{MC'}}{{SC}} = \frac{{FM}}{{FC}} = \frac{{{S_{MAB}}}}{{{S_{ABC}}}}\]

Do đó ta có: \[\frac{{MA'}}{{SA}} + \frac{{MB'}}{{SB}} + \frac{{MC'}}{{SC}} = \frac{{{S_{MBC}}}}{{{S_{ABC}}}} + \frac{{{S_{MAC}}}}{{{S_{ABC}}}} + \frac{{{S_{MAB}}}}{{{S_{ABC}}}} = 1\]