Cho tứ diện ABCD có AB=CD=4,BC=AD=5,AC=BD=6. M là điểm thay đổi trong tâm giác ABC. Các đường thẳng qua M song song với AD,BD,CD tương ứng cắt mặt phẳng (BCD),(ACD),(ABD) tại A′,B′...

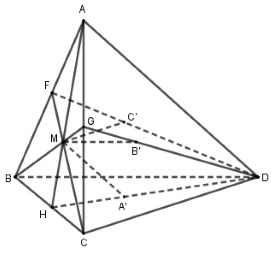
Trong tam giác ABC, kéo dài AM,BM,CM cắt các đoạn thẳng BC,CA,AB lần lượt tại H,G,F.

+) Trong mặt phẳng (HAD), kẻ MA′//AD.

+) Trong mặt phẳng (GBD), kẻ MB′//BD.

+) Trong mặt phẳng (FCD), kẻ MC′//CD.

Từ đó ta được các điểm A′,B′,C′ cần tìm.

Theo định lý Ta – let ta có: \[\frac{{MA'}}{{AD}} = \frac{{HM}}{{HA}} \Rightarrow MA' = 5.\frac{{MH}}{{AH}}\]

\[\frac{{MB'}}{{BD}} = \frac{{GM}}{{GB}} \Rightarrow MB' = 6.\frac{{MG}}{{BG}};\frac{{MC'}}{{CD}} = \frac{{FM}}{{FC}} \Rightarrow MC' = 4.\frac{{MF}}{{CF}}\]

\[ \Rightarrow MA'.MB'.MC' = 120.\frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}}\]

Trong tam giác ABC ta có:\[1 = \frac{{MH}}{{AH}} + \frac{{MG}}{{BG}} + \frac{{MF}}{{CF}} \ge 3\sqrt[3]{{\frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}}}}\]

\[ \Rightarrow \frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}} \le \frac{1}{{27}}\]

Do đó\[MA'.MB'.MC' = 120.\frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}} \le 120.\frac{1}{{27}} = \frac{{40}}{9}\]

\[ \Rightarrow {\left( {MA'.MB'.MC'} \right)_{\max }} = \frac{{40}}{9}\]