Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC) . Khẳng định nào sau đây là đúng?

* Hướng dẫn giải

Vì \[S \in \left( {SAD} \right)\] và\[S \in \left( {SBC} \right)\] nên\[S \in d\]

Ta có: \(\left\{ {\begin{array}{*{20}{c}}{AD \subset (SAD)}\\{BC \subset (SBC)}\\{AD//BC}\\{d = (SAD) \cap (SBC)}\end{array}} \right. \Rightarrow d//AD//BC\)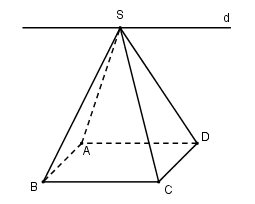

Đáp án cần chọn là: A