Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm điều kiện của AB và C...

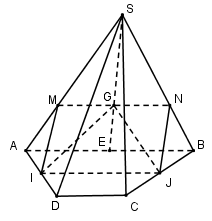
Ta có: ABCD  là hình thang và I,J là trung điểm của AD và BC  nên IJ là đường trung bình của hình thang ABCD.

\[ \Rightarrow IJ//AB//CD\]

\(\left\{ {\begin{array}{*{20}{c}}{G \in (SAB) \cap (IJG)}\\{AB \subset (SAB)}\\{IJ \subset (IJG)}\\{AB//IJ}\end{array}} \right. \Rightarrow \) Trong (SAB) qua G  kẻ\[MN//AB\left( {M \in SA;N \in SB} \right)\]

\[ \Rightarrow \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) = MN\] và\[MN//IJ//AB//CD\]

Dễ thấy thiết diện của (IJG) và hình chóp là hình thang MNJI.

G  là trọng tâm của tam giác SAB  và MN//AB nên theo định lí Ta-let ta có:

\[\frac{{MN}}{{AB}} = \frac{{SG}}{{SE}} = \frac{2}{3}\] (Với E  là trung điểm của AB).

\[ \Rightarrow MN = \frac{2}{3}AB\]

Lại có: IJ là đường trung bình của hình thang ABCD  nên\[{\rm{IJ}} = \frac{{AB + CD}}{2}.\]

Để hình thang MNJI  trở thành hình bình hành thì cần điều kiện MN=IJ.

\[ \Rightarrow \frac{2}{3}AB = \frac{1}{2}\left( {AB + CD} \right) \Leftrightarrow \frac{1}{6}AB = \frac{1}{2}CD \Leftrightarrow AB = 3CD.\]