Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a, SA=SD=3a, SB=SC=

* Hướng dẫn giải

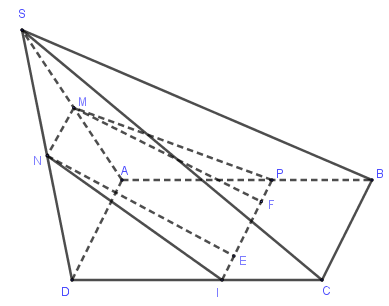
Do MN//AD⇒MN//BC. Vậy (MNP) cắt mặt phẳng (ABCD) theo giao tuyến đi qua P, song song BC và cắt DC tại điểm I. Thiết diện của khối chóp cắt bởi mặt phẳng (MNP) chính là hình thang MNIP.

Do \[\Delta NDI = \Delta MAP\;\] nên MP=NI. Từ đó suy ra MNIP là hình thang cân.

Trong tam giác SAB, ta có

\[\cos \widehat {SAB} = \frac{{S{A^2} + A{B^2} - S{B^2}}}{{2.SA.AB}} = \frac{{9{a^2} + 9{a^2} - 27{a^2}}}{{2.3a.3a}} = - \frac{{9{a^2}}}{{18{a^2}}} = - \frac{1}{2}\]

Trong tam giác MAP, ta có

\[M{P^2} = M{A^2} + A{P^2} - 2MA.AP.\cos \widehat {MAP} = \frac{{9{a^2}}}{4} + 4{a^2} + \frac{{3a}}{2} \cdot 2a = \frac{{37{a^2}}}{4} \Rightarrow MP = \frac{{a\sqrt {37} }}{2}\]

Từ M kẻ \[MF \bot PI\], từ N kẻ \[NE \bot PI\].

Dễ thấy, tứ giác MNEF là hình chữ nhật và từ đó suy ra

\[MN = EF = \frac{{3a}}{2} \Rightarrow PF = EI = \frac{{3a}}{4}\]

Xét tam giác vuông MFP, ta có

\[MF = \sqrt {M{P^2} - F{P^2}} = \sqrt {\frac{{37{a^2}}}{4} - \frac{{9{a^2}}}{{16}}} = \frac{{a\sqrt {139} }}{4}\]

Ta có

\[{S_{MNIP}} = \frac{{\left( {MN + IP} \right).MF}}{2} = \frac{{\left( {\frac{{3a}}{2} + 3a} \right) \cdot \frac{{a\sqrt {139} }}{4}}}{2} = \frac{{9{a^2}\sqrt {139} }}{{16}}\]

Đáp án cần chọn là: D