Cho tứ diện ABCD có AB=a, CD=b. Gọi I, J lần lượt là trung điểm AB và CD, giả sử AB

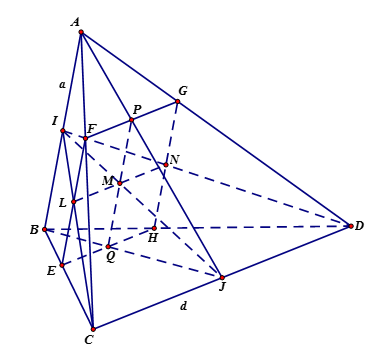
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//CD}\\{CD \subset (ICD)}\\{M \in (\alpha ) \cap (ICD)}\end{array}} \right.\) ⇒ giao tuyến của (α) với (ICD) là đường thẳng qua M và

song song với CDcắt IC tại L và ID tại N.

\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//AB}\\{AB \subset (JAB)}\\{M \in (\alpha ) \cap (JAB)}\end{array}} \right.\) ⇒ giao tuyến của (α) với (JAB) là đường thẳng qua M và song song

với AB cắt JA tại P và JB tại Q.

Ta có\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//AB}\\{AB \subset (ABC)}\\{L \in (\alpha ) \cap (ABC)}\end{array}} \right. \Rightarrow EF//AB\,\,\,\,\left( 1 \right)\)

Tương tự \(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//AB}\\{AB \subset (ABD)}\\{N \in (\alpha ) \cap (ABD)}\end{array}} \right. \Rightarrow HG//AB\,\,\left( 2 \right)\)

Từ  (1) và (2) \[ \Rightarrow EF//HG//AB\,\,\,\left( 3 \right)\]

Ta có\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//CD}\\{CD \subset (ACD)}\\{P \in (\alpha ) \cap (ACD)}\end{array}} \right. \Rightarrow FG//CD\,\,\,\left( 4 \right)\)

Tương tự\(\left\{ {\begin{array}{*{20}{c}}{(\alpha )//CD}\\{CD \subset (BCD)}\\{Q \in (\alpha ) \cap (BCD)}\end{array}} \right. \Rightarrow EH//CD\,\,\,\left( 5 \right)\)

Từ  (4) và (5) \[ \Rightarrow FG//EH//CD\,\,\,\,\left( 6 \right)\]

Từ  (3) và (6), suy ra EFGH là hình  bình hành. Mà AB⊥CD nên EFGH là hình chữ nhật.

Xét tam giác ICD có:\[LN//CD \Rightarrow \frac{{LN}}{{CD}} = \frac{{IN}}{{ID}}\]

Xét tam giác ICD có:\[MN//JD \Rightarrow \frac{{IN}}{{ID}} = \frac{{IM}}{{IJ}}\]

Do đó\[\frac{{LN}}{{CD}} = \frac{{IM}}{{IJ}} = \frac{1}{3} \Rightarrow LN = \frac{1}{3}CD = \frac{b}{3}\]

Tương tự\[\frac{{PQ}}{{AB}} = \frac{{JM}}{{JI}} = \frac{2}{3} \Rightarrow PQ = \frac{2}{3}AB = \frac{{2a}}{3}\]

Vậy\[{S_{EFGH}} = PQ.LN = \frac{{2ab}}{9}\]