Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, các cạnh bên bằng

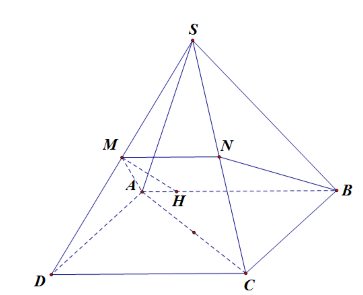
Gọi Δ là giao tuyến của mặt phẳng (ABM) với mặt phẳng (SDC).

Ta có AB song song với (SDC) nên suy ra AB song song với Δ.

Gọi N là trung điểm SC, ta có \[N \in \Delta \].

Do đó thiết diện là hình thang cân ABNM.

Kẻ \[MH \bot AB\;\] tại H, \[H \in AB\]

Do AB=CD và MN

Áp dụng công thức độ dài đường trung tuyến, ta có

\[AM = \sqrt {\frac{{{a^2} + 2{a^2}}}{2} - \frac{{2{a^2}}}{4}} = a\]

Mặt khác \[AH = \frac{{AB - MN}}{2} = \frac{{a - \frac{a}{2}}}{2} = \frac{a}{4}\] nên

\[MH = \sqrt {A{M^2} - A{H^2}} = \frac{{a\sqrt {15} }}{4}\]

Suy ra\[{S_{ABNM}} = \frac{{MH.\left( {MN + AB} \right)}}{2} = \frac{{3\sqrt {15} {a^2}}}{{16}}\]