Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết mặt phẳng (SBC) tạo với đáy một góc 60 độ và M là trung điểm của SD. Tính kho...

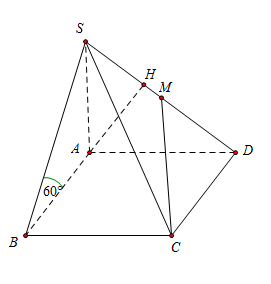
Ta có\(\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot (SAB)\)

\[ \Rightarrow \widehat {SBA}\] là góc giữa 2 mặt phẳng (SBC) và (ABC)

Ta có \[SA = AB\tan \widehat {SBA} = a\sqrt 3 \]

Do AB||CD do đó\[d\left( {AB;CM} \right) = d\left( {AB;\left( {CMD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\]

Dựng\[AH \bot SD\,\,\,\left( 1 \right)\] ta có:

\(\left\{ {\begin{array}{*{20}{c}}{CD \bot AD}\\{CD \bot SA}\end{array}} \right. \Rightarrow CD \bot (SAD) \Rightarrow CD \bot AH(2)\)

Từ (1) và (2)\[ \Rightarrow AH \bot \left( {SCD} \right)\]

khi đó\[d\left( {A;\left( {SCD} \right)} \right) = AH\]

Lại có\[AH = \frac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \frac{{a\sqrt 3 }}{2}.\]

Do đó\[d = \frac{{a\sqrt 3 }}{2}.\]