Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, gọi I là trung điểm của AB. Hình chiếu vuông góc của S trên mặt đáy là trung điểm của CI. Biết chiều cao của khối chóp là

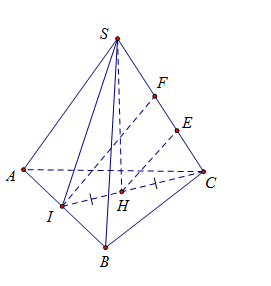
Ta có \(\left\{ {\begin{array}{*{20}{c}}{CI \bot AB}\\{SH \bot AB}\end{array}} \right. \Rightarrow AB \bot (SIC)\)

Dựng\[IF \bot SC\,\,\left( 1 \right)\] khi đó\[IF \subset \left( {SIC} \right) \Rightarrow IF \bot AB\,\,\left( 2 \right)\] do đó  IF là đoạn vuông góc chung của AB và SC. Dựng \[HE \bot SC \Rightarrow HE//IF\] ta có\[HE = \frac{1}{2}IF\]

Lại có\[CI = \frac{{a\sqrt 3 }}{2} \Rightarrow CH = \frac{{a\sqrt 3 }}{4}\]

Khi đó\[HE = \frac{{SH.HC}}{{\sqrt {S{H^2} + C{H^2}} }} = \frac{{a\sqrt 3 .\frac{{a\sqrt 3 }}{4}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}} }} = \frac{{a\sqrt {51} }}{{17}} \Rightarrow IF = \frac{{2a\sqrt {51} }}{{17}}\]