Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác vuông cân, AC=BC=3a. Hình chiếu vuông góc của B′ lên mặt đáy trùng với trọng tâm của tam giác ABC, mặt phẳng (ABB′A′) tạo với mặ...
Câu hỏi :
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác vuông cân, AC=BC=3a. Hình chiếu vuông góc của B′ lên mặt đáy trùng với trọng tâm của tam giác ABC, mặt phẳng (ABB′A′) tạo với mặt phẳng (ABC) một góc 600. Tính khoảng cách giữa hai đường thẳng AB và B′C.
A.\[d = \frac{{3a\sqrt {42} }}{{14}}.\]
B. \[d = \frac{{3a\sqrt {42} }}{7}.\]
C. \[d = \frac{{a\sqrt {42} }}{4}.\]
D. \[d = \frac{{a\sqrt {42} }}{7}.\]
* Đáp án
* Hướng dẫn giải
Gọi G là trọng tâm tam giác ABC thì\[B'G \bot \left( {ABC} \right)\]
Dựng\[CI \bot AB\] suy ra I là trung điểm của AB.
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{AB \bot B\prime G}\\{AB \bot GI}\end{array}} \right. \Rightarrow AB \bot (B\prime GI) \Rightarrow (\widehat {(ABB\prime A\prime );(ABC)}) = \widehat {B\prime IG} = {60^0}\)
Lại có\[CI = \frac{1}{2}AB = \frac{{3a\sqrt 2 }}{2} \Rightarrow GI = \frac{1}{3}CI = \frac{{a\sqrt 2 }}{2}\]
\[ \Rightarrow B'G = GI.\tan {60^0} = \frac{{a\sqrt 6 }}{2}\]
Dựng\[IH \bot B'C\] ta có\[IH \subset \left( {B'IC} \right)\] mà \[AB \bot \left( {B'IC} \right) \Rightarrow IH \bot AB\]
\[ \Rightarrow d\left( {AB;B'C} \right) = IH = \frac{{B'G.CI}}{{B'C}}\]
Ta có :
\[B'C = \sqrt {B'{G^2} + G{C^2}} = \sqrt {\frac{{3{a^2}}}{2} + 2{a^2}} = \frac{{a\sqrt {14} }}{2} \Rightarrow IH = \frac{{3a\sqrt {42} }}{{14}}\]
Do đó\[d = IH = \frac{{3a\sqrt {42} }}{{14}}\]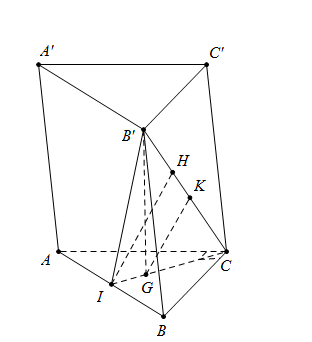
Đáp án cần chọn là: A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Khoảng cách giữa hai đường thẳng chéo nhau !!
Copyright © 2021 HOCTAP247
