Cho hình lăng trụ đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Khoảng cách giữa hai đường thẳng AM và B’C là :

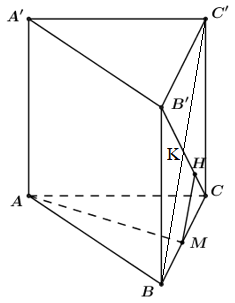
Ta có :\(\left\{ {\begin{array}{*{20}{c}}{AM \bot BC}\\{AM \bot BB\prime }\end{array}} \right. \Rightarrow AM \bot (BCC\prime B\prime )\)

Trong \[\left( {BCC'B'} \right)\] kẻ\[MH//BC'\,\,\left( {H \in B'C} \right) \Rightarrow MH \bot B'C\]

\[MH \subset \left( {BCC'B'} \right) \Rightarrow AM \bot MH\]

\[ \Rightarrow MH\] là đoạn vuông góc chung giữa AM và B’C\[ \Rightarrow d\left( {AM;B'C} \right) = MH\]

Dễ thấy\[MH = \frac{1}{2}BK = \frac{1}{4}B'C = \frac{{a\sqrt 2 }}{4}\]  với K là trung điểm của B′C.\[ \Rightarrow d\left( {AM;B'C} \right) = \frac{{a\sqrt 2 }}{4}\]