Cho tứ diện đều ABCD có cạnh bằng 2a. Khoảng cách giữa hai đường thẳng AB và CD là

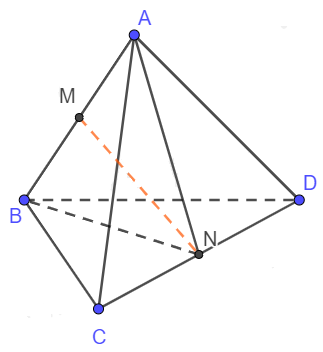
Bước 1: Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh MN là đoạn vuông góc chung của AB và CD.

Gọi M, N lần lượt là trung điểm của AB và CD. 

\[{\rm{\Delta }}BCD,{\rm{\Delta }}ACD\] đều nên:

\(\left. {\begin{array}{*{20}{c}}{AN \bot CD}\\{BN \bot CD}\end{array}} \right\} \Rightarrow (ABN) \bot CD \Rightarrow MN \bot CD\)

Tương tự ta có \[MN \bot AB\]

Khoảng cách giữa 2 đường thẳng AB, CD là độ dài của MN.

Bước 2: Tính MN.

\[{\rm{\Delta }}ACD\] đều cạnh 2a; AN là đường cao.

\[ \to AN = AC.\frac{{\sqrt 3 }}{2} = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 \]

\[AM = \frac{1}{2}AB = a\]

\[{\rm{\Delta }}AMN\] vuông tại M\[MN \bot AB\]  nên:

\[MN = \sqrt {A{N^2} - A{M^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \]