Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AB=2a,AD=DC=a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng 60 độ. Tính khoả...

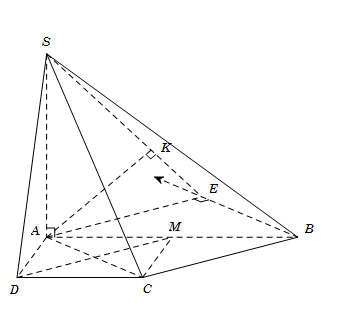
\(\left\{ {\begin{array}{*{20}{c}}{(SAB) \bot (ABCD)}\\{(SAD) \bot (ABCD)}\\{(SAB) \cap (SAD) = SA}\end{array}} \right. \Rightarrow SA \bot (ABCD)\)

Xác định

\[{60^0} = \widehat {\left( {SC;\left( {ABCD} \right)} \right)}\]

\[ = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}\]

và \[SA = AC.\tan \widehat {SCA} = \sqrt {A{D^2} + C{D^2}} .\tan {60^0} = a\sqrt 2 .\sqrt 3 = a\sqrt 6 .\]

Gọi M là trung điểm AB, suy ra ADCM là hình vuông nên CM=AD=a.

Xét tam giác ACB, ta có trung tuyến\[CM = a = \frac{1}{2}AB\] nên tam giác ACB vuông tại C.

Lấy điểm E sao cho ACBE là hình chữ nhật, suy ra \[AC\parallel BE\]  và E nằm trong (ABCD).

Do đó \[d\left( {AC;SB} \right) = d\left( {AC;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right)\]

Kẻ \[AK \bot SE\,\,\,\left( 1 \right)\]  ta có:\(\left\{ {\begin{array}{*{20}{c}}{BE \bot AE}\\{BE \bot SA}\end{array}} \right. \Rightarrow BE \bot (SAE) \Rightarrow BE \bot AK(2)\)

Từ (1) và (2) \[ \Rightarrow AK \bot \left( {SBE} \right)\]

Khi đó \[d\left( {A,\left( {SBE} \right)} \right) = AK = \frac{{SA.AE}}{{\sqrt {S{A^2} + A{E^2}} }}.\]

Ta có:\[AE = BC = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \Rightarrow AK = \frac{{a\sqrt 6 .a\sqrt 2 }}{{\sqrt {6{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{2}\]