Cho hình lăng trụ ABC.A′B′C′ có tam giác ABC vuông tại A, AB=a,

* Hướng dẫn giải

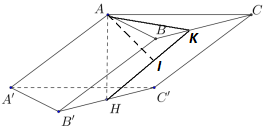
Bước 1:

Ta có\[AA'//BB' \Rightarrow AA'//\left( {BCC'B'} \right) \supset BC'\]

\[ \Rightarrow d\left( {AA';BC'} \right) = d\left( {AA';\left( {BCC'B'} \right)} \right) = d\left( {A;\left( {BCC'B'} \right)} \right)\]

Bước 2:

Trong (ABC) kẻ \[AK \bot BC\,\,\left( {K \in BC} \right)\]  trong (AHK) kẻ \[AI \bot HK\,\,\left( {I \in HK} \right)\] ta có:

\(\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{BC \bot AK}\\{BC \bot AH}\end{array} \Rightarrow BC \bot (AHK) \Rightarrow BC \bot AI} \right.\\\left\{ {\begin{array}{*{20}{c}}{AI \bot HK}\\{AI \bot BC}\end{array}} \right. \Rightarrow AI \bot (BCC\prime B\prime )\end{array}\)

\[ \Rightarrow d\left( {A;\left( {BCC'B'} \right)} \right) = AI = d\left( {AA';BC'} \right)\]

Bước 3:

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có

\[AK = \frac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \frac{{a.a\sqrt 3 }}{{\sqrt {{a^2} + 3{a^2}} }} = \frac{{a\sqrt 3 }}{2}\]

Tam giác A′B′C′ có \[B'C' = \sqrt {A'{B^{\prime 2}} + A'{C^{\prime 2}}} = 2a \Rightarrow A'H = \frac{1}{2}B'C' = a\]

\[ \Rightarrow AH = \sqrt {A{A^{\prime 2}} - A'{H^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \]

Áp dụng hệ thức lượng trong tam giác vuông AHK ta có

\[AI = \frac{{AH.AK}}{{\sqrt {A{H^2} + A{K^2}} }} = \frac{{a\sqrt 3 .\frac{{a\sqrt 3 }}{2}}}{{\sqrt {3{a^2} + \frac{{3{a^2}}}{4}} }} = \frac{{a\sqrt {15} }}{5}\]

Vậy\[d\left( {AA';BC'} \right) = \frac{{a\sqrt {15} }}{5}\]

Vậy m=15.