Cho tứ diện gần đều ABCD, biết [AB = CD = 5,AC = BD =

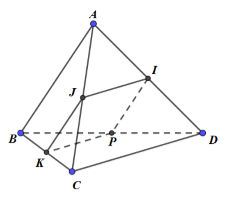
Gọi I, J, K, P lần lượt là trung điểm của AD, AC, BC, BD.

Khi đó, AB // IP // JK, CD // IJ // KP

\[ \Rightarrow \left( {\widehat {AB;CD}} \right) = \left( {\widehat {IP;KP}} \right)\]

Ta có:\[KP = \frac{1}{2}CD = \frac{5}{2},IP = \frac{1}{2}AB = \frac{5}{2}\]

\[A{K^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4} = \frac{{25 + 34}}{2} - \frac{{41}}{4} = \frac{{77}}{4} = D{K^2}\]

Tam giác AKD cân tại K, KI là trung tuyến

\[ \Rightarrow KI \bot AD \Rightarrow I{K^2} = A{K^2} - A{I^2} = \frac{{77}}{4} - \frac{{41}}{4} = 9\]

\[\cos \widehat {IPK} = \frac{{I{P^2} + K{P^2} - I{K^2}}}{{2.IP.KP}} = \frac{{\frac{{25}}{4} + \frac{{25}}{4} - 9}}{{2.\frac{5}{2}.\frac{5}{2}}} = \frac{7}{{25}} > 0 \Rightarrow \widehat {IPK} < {90^0}\]

\[ \Rightarrow \left( {\widehat {AB;CD}} \right) = \left( {\widehat {IP;KP}} \right) = \widehat {IPK} \Rightarrow \sin \left( {\widehat {AB;CD}} \right) = \sin \widehat {IPK} = \sqrt {1 - {{\left( {\frac{7}{{25}}} \right)}^2}} = \frac{{24}}{{25}}\]