Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc

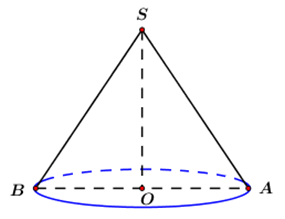
Thiết diện qua trục của hình nón là \[\Delta SAB\] vuông cân tại \[S\] và có \(SA = SB = a\).

\( \Rightarrow l = SA = a\)

Ta có: \(\Delta SAB\) vuông cân tại \(S\) \( \Rightarrow AB = SA\sqrt 2 = a\sqrt 2 \)

\( \Rightarrow r = OA = \frac{1}{2}AB = \frac{{a\sqrt 2 }}{2}\)

\( \Rightarrow \) Diện tích xung quanh của hình nón đã cho là: \({S_{xq}} = \pi rl = \pi .\frac{{a\sqrt 2 }}{2}.a = \frac{{\pi {a^2}\sqrt 2 }}{2}\).