Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 0; 1), B(0; 1; -1)

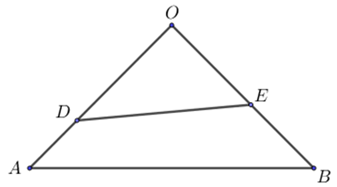
Ta có: \(\overrightarrow {OA} = \left( {1;0;1} \right),\;\overrightarrow {OB} = \left( {0;1; - 1} \right),\;OA = OB = \sqrt 2 ,\) \(\overrightarrow {AB} = \left( { - 1;1; - 2} \right),\;AB = \sqrt 6 .\)

Suy ra: \(\frac{{{S_{ODE}}}}{{{S_{OAB}}}} = \frac{{OD.OE}}{{OA.OB}} \Leftrightarrow \frac{1}{2} = \frac{{OD.OE}}{2} \Leftrightarrow OD.OE = 1.\)

Lại có \(\cos \widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{2 + 2 - 6}}{4} = \frac{{ - 1}}{2}.\)

Mặt khác \(D{E^2} = O{D^2} + O{E^2} - 2OD.OE\cos \widehat {AOB} = O{D^2} + O{E^2} + OD.OE \ge 3OD.OE.\)

\( \Rightarrow DE \ge \sqrt 3 \). Dấu bằng xảy ra khi \(OD = OE = 1\)

Khi đó \(\overrightarrow {OD} = \frac{{\sqrt 2 }}{2}.\overrightarrow {OA} \Rightarrow D\left( {\frac{{\sqrt 2 }}{2};0;\frac{{\sqrt 2 }}{2}} \right),\;\overrightarrow {OE} = \frac{{\sqrt 2 }}{2}.\overrightarrow {OB} \Rightarrow E\left( {0;\frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right).\)

Vậy trung điểm \(I\) của \(DE\) có tọa độ \(I\left( {\frac{{\sqrt 2 }}{4};\frac{{\sqrt 2 }}{4};0} \right)\).